複雑な図形の断面二次モーメントを求める際は、断面二次モーメントを足したり引いたりする手法がよく用いられます。しかし、単純に足し引きをするだけでは答えが合わない場合もあります。今回は断面二次モーメントの足し引きをする際の注意点について解説します。
長方形断面の断面二次モーメント
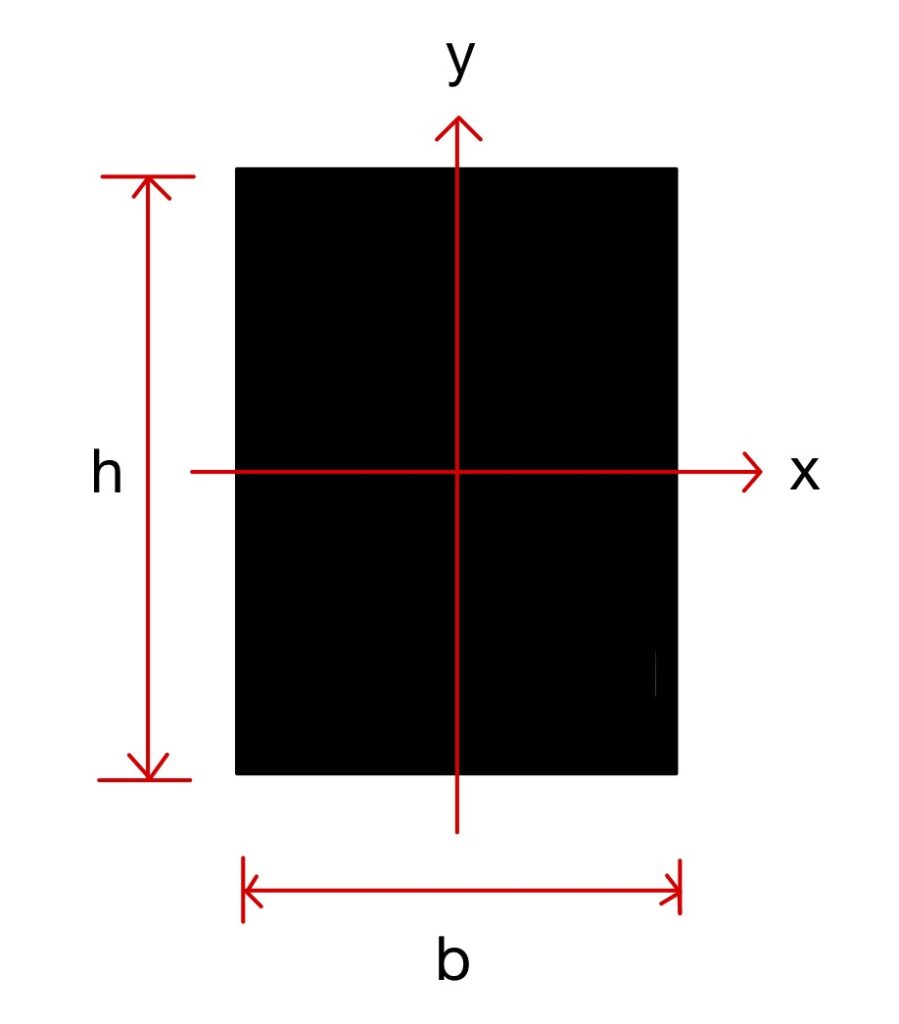
上図のような長方形断面の断面二次モーメントは以下の式で表されます。
x軸まわりの断面二次モーメント$I_x=\frac{bh^3}{12}$
y軸まわりの断面二次モーメント$I_y=\frac{b^3h}{12}$
今回のキーポイントとなるのは、何軸まわりの断面二次モーメントを求めるかです。また、上の式に加えて、平行軸の定理についても理解する必要があります。
平行軸の定理
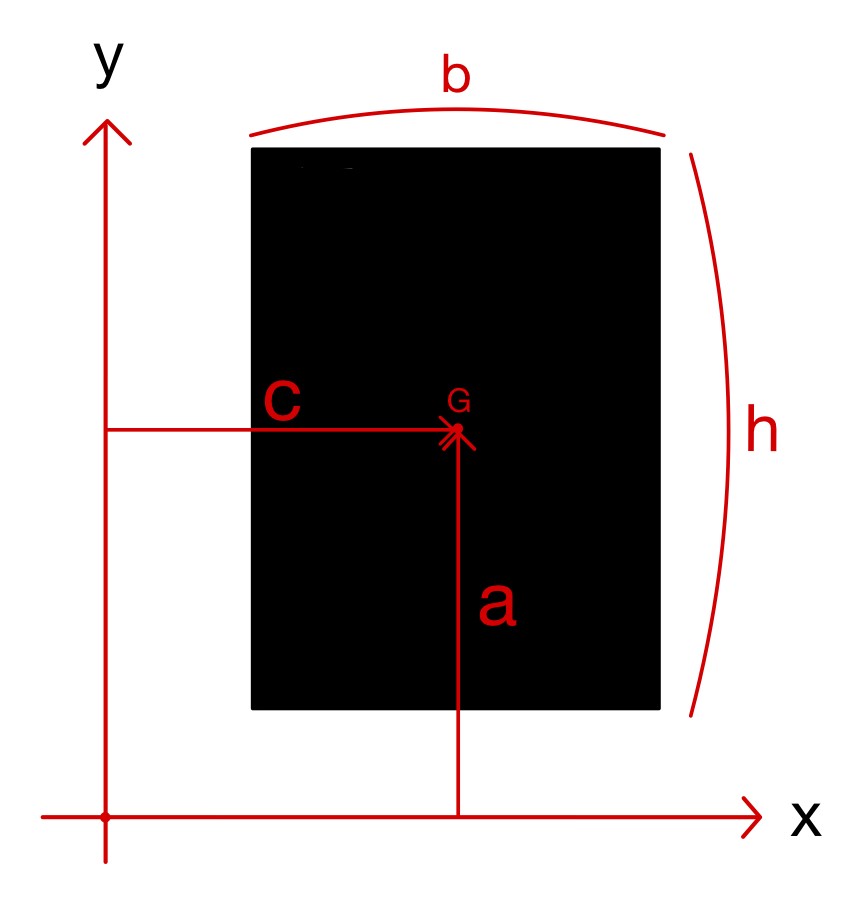
上図のように、図心Gと軸にずれが生じている場合の断面二次モーメントを求める際は平行軸の定理を用いる必要があります。平行軸の定理を使用した場合の断面二次モーメントは以下の式となります。
x軸まわりの断面二次モーメント$I_x=a^2A+I_X$
y軸まわりの断面二次モーメント$I_y=c^2A+I_Y$
ここで、a,cは図心とそれぞれの軸とのずれ、Aは面積(A=bh)、$I_X$,$I_Y$は図心と軸のずれを考慮しない場合の断面二次モーメント($I_X=\frac{bh^3}{12}$,$I_Y=\frac{b^3h}{12}$)とします。
平行軸の定理は、図心と軸のずれを考慮しない場合の断面二次モーメントに、(図心と軸のずれの2乗×面積)を足したもの
このように図心と軸にずれが生じている場合は平行軸の定理を使う必要があることを頭にとどめておいてください。
例1 基本
ここから本題に入ります。まずは簡単な図形の断面二次モーメントを求めてみましょう。
例1:以下の図のx軸まわりの断面二次モーメントを求める(黒い箇所)。
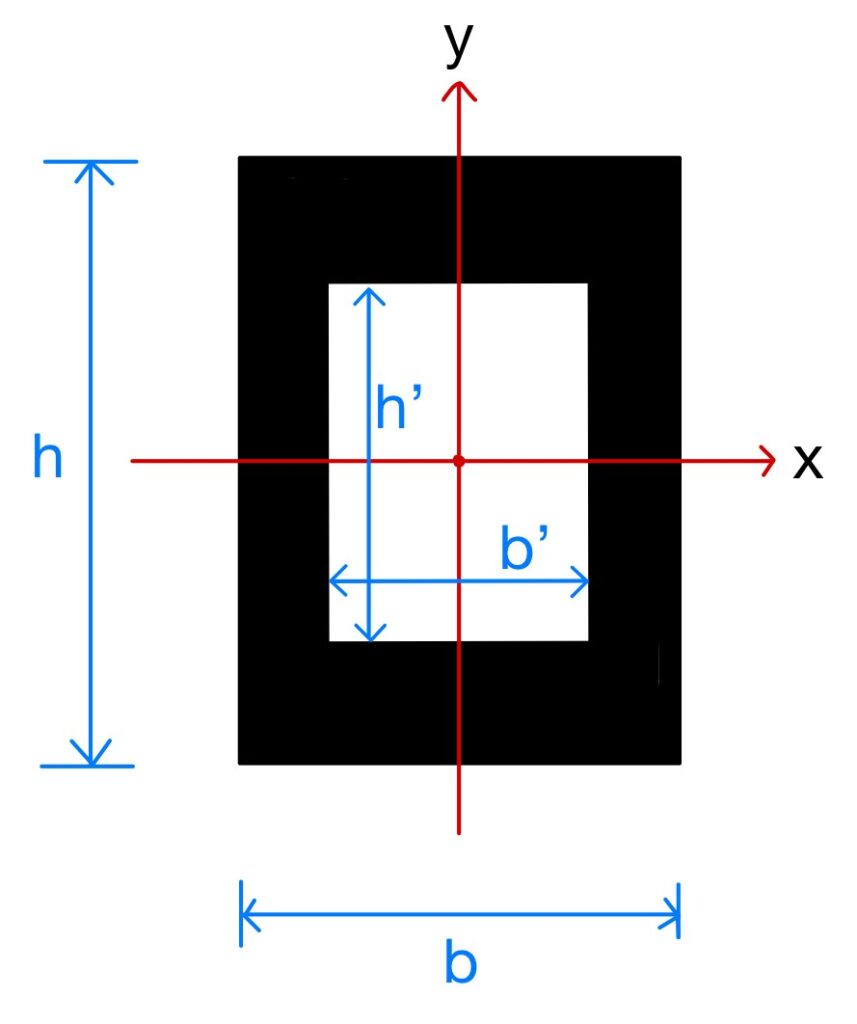
こちらの図形の断面二次モーメントは図心のずれがないため、黒い長方形の断面二次モーメントから白い長方形の断面二次モーメントを引くだけで求まります。
黒い長方形の断面二次モーメント=$\frac{bh^3}{12}$
白い長方形の断面二次モーメント=$\frac{b’h’^3}{12}$
よって上図の断面二次モーメントは「$I_x=\frac{bh^3-b’h’^3}{12}$」と簡単に求めることができます。
例2 I形
I形図形の断面二次モーントも足し引きだけで求めることが可能ですが、足して求めるのか引いて求めるのか注意が必要となります。
例2:以下の図形のx軸およびy軸まわりの断面二次モーメントを求める。
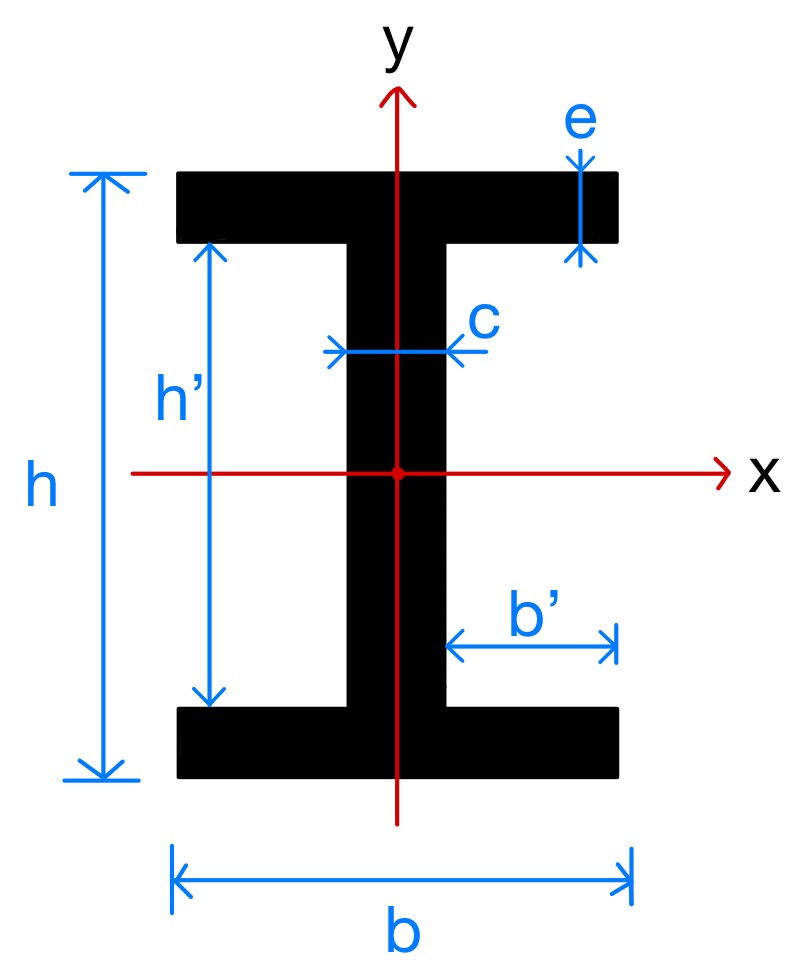
I形図形の断面二次モーメントは以下の2通りの方法で求めることができます。
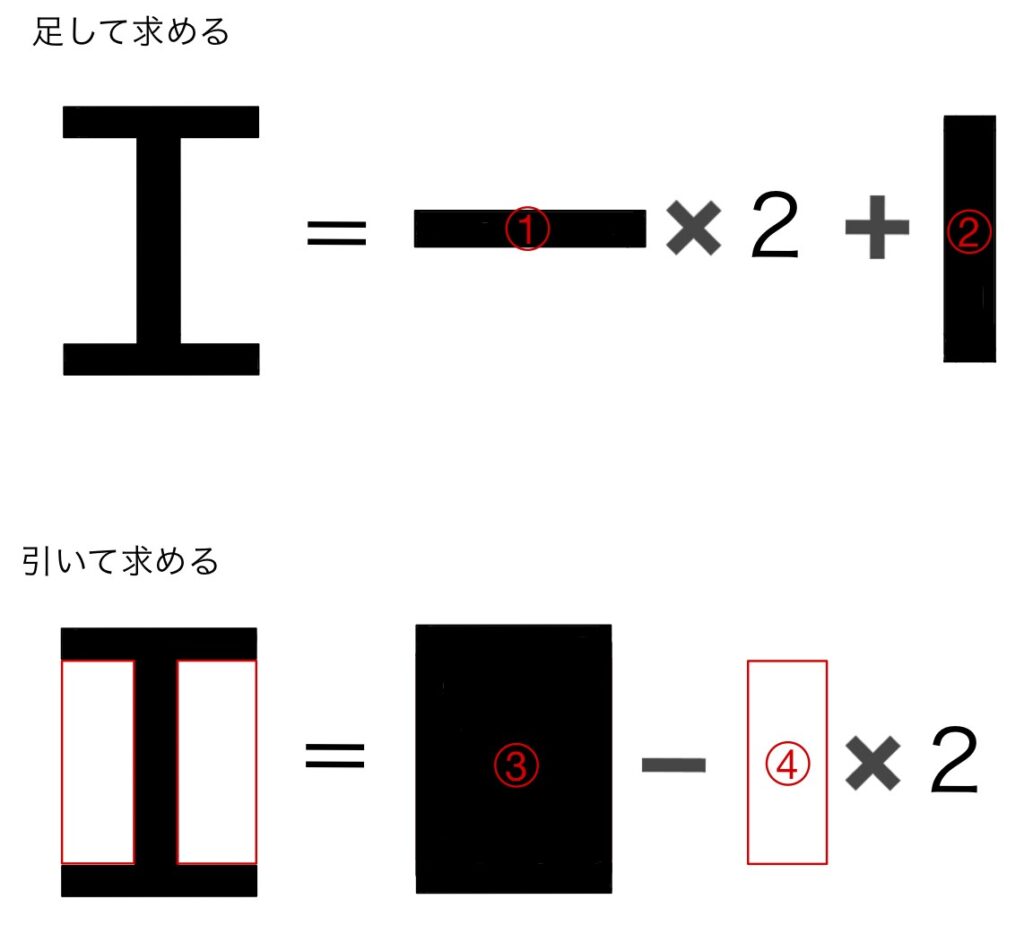
x軸まわりの断面二次モーメント
まずはx軸まわりの断面二次モーメントを求めてみます。
・足して求める場合
x軸まわりの断面二次モーメントを求めるので、まずはx軸と各図形の図心のずれを確認します。①の図形の図心はx軸上にはなく(ずれ:$\frac{h’}{2}+\frac{e}{2}$)、②の図形の図心はx軸上にあることが確認できます。よって、①の図形に関しては平行軸の定理を用いる必要があり、このことを踏まえて式を立てると以下のようになります。
$I_x=((\frac{h’+e}{2})^2×be+\frac{be^3}{12})×2+\frac{ch’^3}{12}$
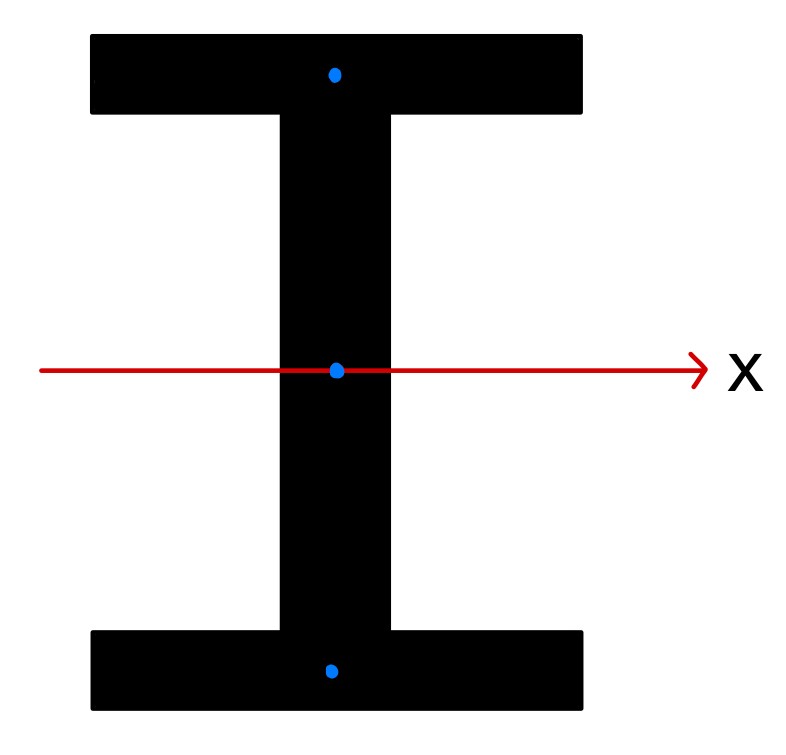
・引いて求める場合
引いて求める場合も同様に図心のずれを確認しますが、こちらはずれがなく、以下のように簡単に断面二次モーメントを求めることができます。
$I_x=\frac{bh^3}{12}-(\frac{b’h’^3}{12})×2$
このように平行軸の定理を用いない式の方が簡単に求めることができます。また、足して求める場合と引いて求める場合で出てくる式は異なりますが、それぞれに値を代入すると同じ結果が得られますのでぜひ試してみてください。
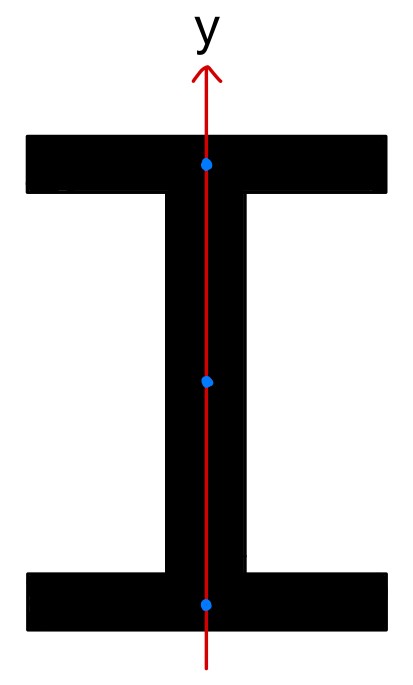
y軸まわりの断面二次モーメント
次はy軸まわりの断面二次モーメントを求めてみます。手順としてはx軸まわりの断面二次モーメントを求めるときと同じです。
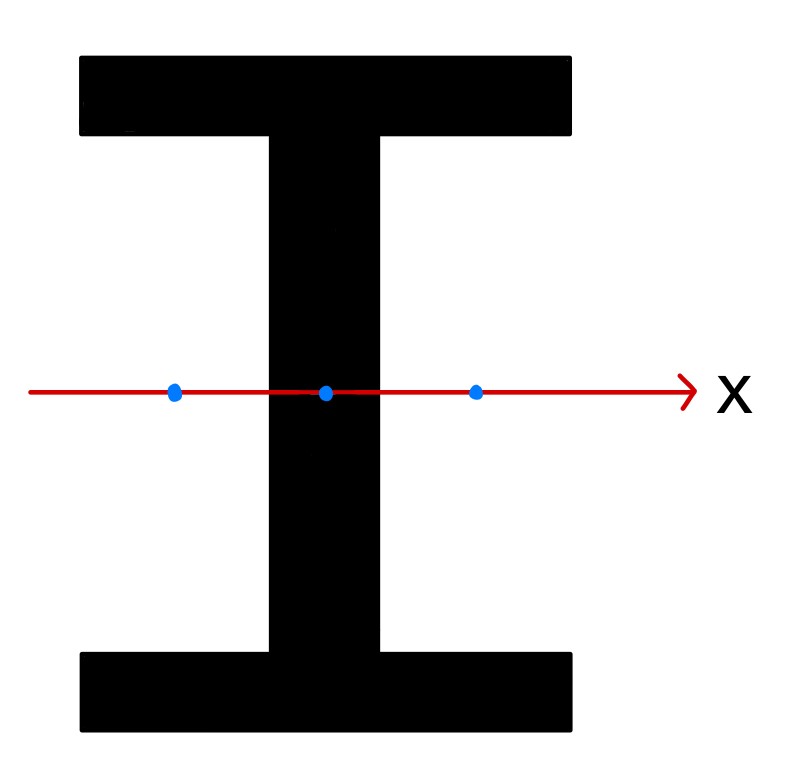
・足して求める場合
まずはy軸と図心のずれを確認します。上図より、足して求める場合は図心のずれがないことが確認できます。よって断面二次モーメントは以下のように求めることができます。
$I_y=(\frac{b^3e}{12})×2+\frac{c^3h’}{12}$
・引いて求める場合
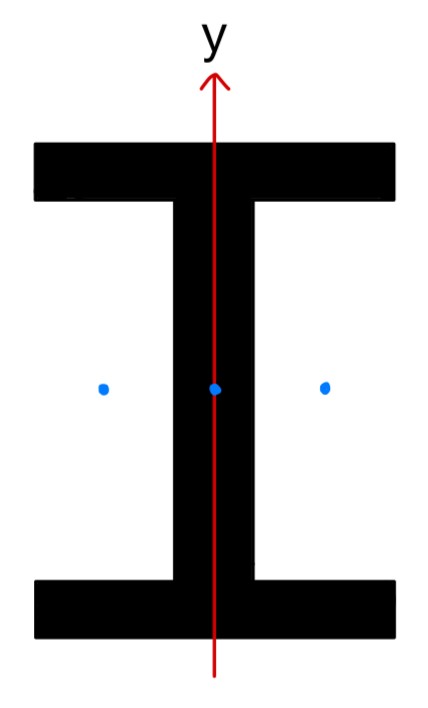
引いて求める場合も同様に図心のずれを確認しましょう。上図より、④の図形の図心はy軸上にはなく、平行軸の定理を用いる必要があることを確認できます。また、このときのずれは$(\frac{c}{2}+\frac{b’}{2})$となります(面積は$b’h’$)。③の図形に関しては図心のずれが生じていないので、これらをもとに断面二次モーメントを求めると以下のようになります。
$I_y=\frac{b^3h}{12}-((\frac{c+b’}{2})^2×b’h’+\frac{b’^3h’}{12})×2$
y軸まわりの断面二次モーメントは、x軸まわりの断面二次モーメントを求めるときと異なり、足して求める方が楽であることが分かります。また、x軸まわりの断面二次モーメントと同じく、足す場合と引く場合で求まった式が異なりますが、値を代入することで同じ結果を得ることができます。
まとめ
今回紹介したもので大切なのは、「図心と軸のずれ」と「平行軸の定理」です。
断面二次モーメントを足し引きする手法は有名ですが、図心と軸のずれについてはあまり述べられておらず、I形ような図形の断面二次モーメントを求める際に間違った値が出てしまうことがあります。例1で紹介したような図形だと問題ありませんが、そうでない場合は異なる値が出てしまうので注意が必要です。
後は基本的な式を覚えておけば断面二次モーメントは簡単に求めることができますので、今回解説したことはぜひ頭に入れておいてください。


コメント